Anti wind-up with prescribed-order anti wind-up filter and PI feedback controller
We show in this application how to use hinfstruct to design a PI feedback and a 2nd-order anti-windup (AW) block for a longitudinal rigid aircraft subject magnitude saturations on the control signal. The AW block is used to control the integrator load. In contrast to more conventional approaches, both components are computed simultaneously.

For details refer to J-M. Biannic and P. Apkarian, "Anti-windup design via nonsmooth multi-objective 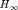 optimization", American Control Conference, San Francisco, 2011
optimization", American Control Conference, San Francisco, 2011
Contents
- Enter plant data
- Simulink diagram
- Build specifications
- Describe composite controller
- Define closed-loop objectives
- Solve
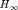 problem with hinfstruct
problem with hinfstruct - Simulate without magnitude saturations (nominal case)
- Simulate with magnitude saturations but without anti-windup (AW off)
- Simulate with magnitude saturations and anti-windup (AW on)
Enter plant data
G = ss([-0.5 1; 0.8 -0.4],[-0.2;-5],eye(2), zeros(2,1) ); m = 1; p = 2;
Simulink diagram

Initialize controller blocks as dummies for linlft
s = tf('s') ;
Kalpha =1; Ki = 1; Kq = 1;
AW = rss(2,1,1);
stepVal = 40; deadZoneWidth = 20;
Build specifications
Enter reference model
s = tf('s'); Ref = (1/(s/4+1))^2; % reference model
Define specification channels using linlft
io = getlinio('AWsyn'); % w, r, alpha, u , e Blocks = {'AWsyn/Kalpha','AWsyn/Ki','AWsyn/Kq','AWsyn/AW'};
Build standard form for performance and robustness
Pperf = linlft('AWsyn',io([2 5]),Blocks); % r -> e perf Probust = linlft('AWsyn',io([1 4 ; 2 5]),Blocks); % (w,r) -> (u,e) robust performance Pu = linlft('AWsyn',io([2 4]),Blocks); % penalize control signal Psim = linlft('AWsyn',io([2 3]),Blocks); % (w,r) -> (u,e) simulation channels
Describe composite controller
Feedback controller as composite of PI and static gains
Kalpha = realp('Kalpha', 0) ; Ki = realp('Ki', 0) ; Kq = realp('Kq', 0) ;
Anti-windup block as 2nd-order state-space model
AW = ltiblock.ss('AW',2,1,1);
Define closed-loop objectives
CLperf = lft(Pperf, blkdiag(Kalpha , Ki , Kq , AW) ) ; % nominal performance CLrobust = lft(Probust, blkdiag(Kalpha , Ki , Kq , AW) ) ; % robust performance CLu = lft(Pu, blkdiag(Kalpha , Ki , Kq , AW) ) ; % realistic control
Add weighting and penalization and aggregate all specs.
W1 = 1/(s/2 + 1) ; pen1 = 70; pen2 = 0.01*pen1; W2=(s+40*0.001)/(s/20+40); H0 = blkdiag( pen1*W1*CLperf , pen2*blkdiag(1, W1)*CLrobust, W2*CLu ) ;
Solve 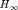 problem with hinfstruct
problem with hinfstruct
op = hinfstructOptions('RandomStart',2); % 2 restarts mean 3 initial points overall [H,gam] = hinfstruct(H0,op) ; gam,
Final: Peak gain = 1.6, Iterations = 48
Final: Peak gain = 1.6, Iterations = 71
Final: Peak gain = 70, Iterations = 5
Spectral abscissa -1.08e-07 is close to bound -1e-07
gam =
1.6033
Recover static gains and dynamic AW blocks
Kalpha = H.Blocks.Kalpha.Value , Ki = H.Blocks.Ki.Value ,
Kq = H.Blocks.Kq.Value , AW = ss(H.Blocks.AW) ;
AWstore = AW; % store anti-windup block
Kalpha = -31.1447 Ki = -66.1159 Kq = -4.8392
Simulate without magnitude saturations (nominal case)
close all; stepVal = 40 ; deadZoneWidth = Inf; figure; sim('AWsyn'); figure(1); clf; subplot(211); plot(alpha.time,alpha.signals.values, yRef.time, yRef.signals.values,'--') ; grid legend('alpha','reference signal'); title(' simulation without magnitude saturations '); subplot(212); plot(u.time,u.signals.values,'--', uSat.time, uSat.signals.values) ; grid legend('control before saturation','saturated control');
Warning: Using a default value of 0.2 for maximum step size. The simulation step size will be equal to or less than this value. You can disable this diagnostic by setting 'Automatic solver parameter selection' diagnostic to 'none' in the Diagnostics page of the configuration parameters dialog
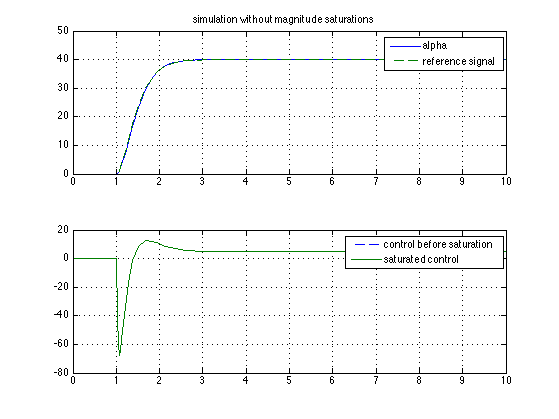
simulation without magnitude saturations
Simulate with magnitude saturations but without anti-windup (AW off)
stepVal = 40 ; deadZoneWidth = 20; figure; AW = 0*AWstore; % no AW sim('AWsyn'); figure(2); clf; subplot(211); plot(alpha.time,alpha.signals.values, yRef.time, yRef.signals.values,'--') ; grid legend('alpha','reference signal'); title(' simulation with magnitude saturations and without AW '); subplot(212); plot(u.time,u.signals.values,'--', uSat.time, uSat.signals.values) ; grid legend('control before saturation','saturated control');
Warning: Using a default value of 0.2 for maximum step size. The simulation step size will be equal to or less than this value. You can disable this diagnostic by setting 'Automatic solver parameter selection' diagnostic to 'none' in the Diagnostics page of the configuration parameters dialog
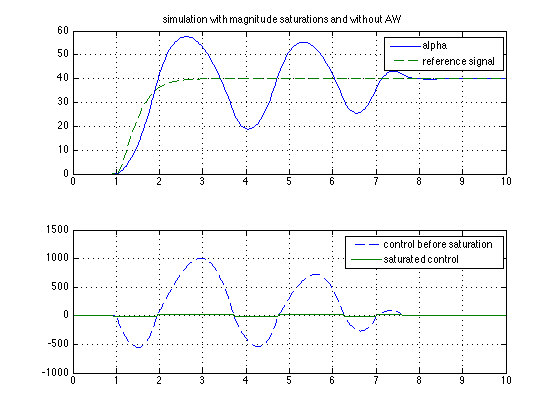
simulation with magnitude saturations and without AW
Simulate with magnitude saturations and anti-windup (AW on)
stepVal = 40 ; deadZoneWidth = 20; figure; AW = AWstore ; % with AW sim('AWsyn'); figure(3); clf; subplot(211); plot(alpha.time,alpha.signals.values, yRef.time, yRef.signals.values,'--') ; grid legend('alpha','reference signal'); title(' simulation with magnitude saturations and AW '); subplot(212); plot(u.time,u.signals.values,'--', uSat.time, uSat.signals.values) ; grid legend('control before saturation','saturated control');
Warning: Using a default value of 0.2 for maximum step size. The simulation step size will be equal to or less than this value. You can disable this diagnostic by setting 'Automatic solver parameter selection' diagnostic to 'none' in the Diagnostics page of the configuration parameters dialog
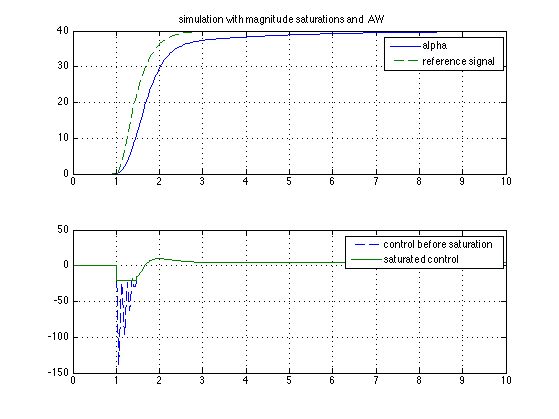
simulation with magnitude saturations and AW