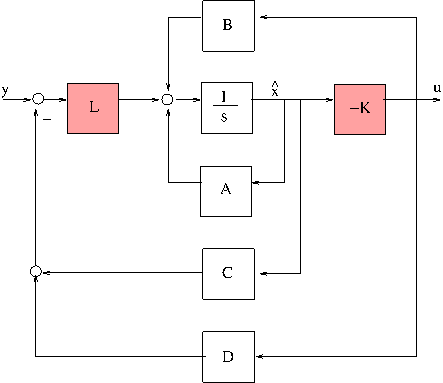
Observer-based controller
A streamlined fashion to define an observer-based controller and solve for it with hinfstruct. We consider the example of the Active Suspension Control from the Robust Control Toolbox, Control Design 1.
Contents
Define augmented plant:
nx = 6; ny = 1; nu = 1; nw = 2; nz = 2;
A = [0 1.0000e+00 0 0 0 0 ;
-5.5800e+01 -3.4483e+00 5.5800e+01 3.4483e+00 0 0;
0 0 0 1.0000e+00 0 0;
2.7427e+02 1.6949e+01 -3.4946e+03 -1.6949e+01 0 0;
0 0 0 0 -5.0000e+02 0;
1.6000e+01 0 0 0 0 -3.1416e+01];
B = [0 0 0;
0 0 3.4483e+01;
0 0 0;
2.2542e+02 0 -1.6949e+02;
0 0 6.4000e+01;
0 0 0];
C = [ 0 0 0 0 -5.4087e+01 0;
0 0 0 0 0 1.5708e+01;
1.0000e+00 0 -1.0000e+00 0 0 0];
D = [0 0 7.6923e+00;
0 0 0;
0 1.0000e-02 0];
P = ss(A,B,C,D);
Define observer-based controller.
P22 = P(nz+(1:ny),nw+(1:nu)) ; [A,B,C,D] = ssdata(P22) ; % u to y plant K = realp('K',zeros(nu,nx)); % state feedback L = realp('L',eye(nx,ny)); % observer gain OBC = ss(A-B*K-L*(C-D*K),L,-K,0) ; % observer-based controller in state-space format
Define closed-loop interconnection
CL0 = lft(P,OBC);
Solve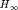 
problem with hinfstruct
[CL,gam1] = hinfstruct(CL0); % CL is tuned version of CL0
Final: Peak gain = 0.609, Iterations = 80
Get state feedback and observer gains
CL.BLocks.K.Value, CL.BLocks.L.Value,
ans =
44.5934 15.6852 -114.5391 0.3011 -2.2210 -54.6811
ans =
1.0e+03 *
0.0206
0.1825
-0.0066
0.5587
-2.2661
0.0270
Compare with hinfsyn (full-order black-box controller).
[K,clp,gam2] = hinfsyn(P,ny,nu) ; % Output achieved objective. fprintf(1,' Achieved H-infinity norms HINFSTRUCT:%6.2f HINFSYN:%6.2f \n\n', gam1,gam2);
Achieved H-infinity norms HINFSTRUCT: 0.61 HINFSYN: 0.61