PID in series with 1st-order roll-off filter

A practical broadly used architecture which accounts for noise attenuation and frequency-domain robustness

Enter process data and derive approximate model
Set performance and roll-off weights
Define augmented plant for mixed sensitivity design
Build controller as a PID with 1st-order roll-off filter
Run hinfstruct
Retrieve results for PID and form aggregate controller
Show step responses of process and approximate model
Check roll-off property

Enter process data and derive approximate model

s = tf('s');
Gprocess =  tf(1,[1 1],'ioDelay',0.5) ; % 1st-order process system with delay
Gmodel   = pade(Gprocess,4);            % pade approximation of process

Set performance and roll-off weights

Performance weight

A = 0.01; % steady-state offset less than A
M = 1.2;  % amplification of high-frequency noise less than M
wB = 1;   % closed-loop bandwith higher than wB
wS = (1/M)*(s/wB + M)/(s/wB + A); % weight

Robustness weight accounts for uncertainty/noise in the high-frequency range

lfG=0.001; % desired low frequency gain
hfG= 40;   % desired high frequency gain
wc=  5 ;   % desired crossover
wT=(s+wc*lfG)/(s/hfG+wc);
%
bodemag(wS,'b-',wT,'r--'); grid; legend('Sensitivity weight','Complementary sensitivity weight');

Define augmented plant for mixed sensitivity design

P = augw(Gmodel,wS,[], wT);  % augmented plant for mixed sensitivity design
%

Build controller as a PID with 1st-order roll-off filter

Cpid = ltiblock.pid('C0','pid');
FrollOff = tf(wc,[1 wc]); % set unit DC gain roll-off filter
Call = FrollOff*Cpid ;    % overall controller as series of blocks
CL0 = lft(P,Call);        % form closed-loop interconnection

Run `hinfstruct`

[CL,gam] = hinfstruct(CL0);

Final: Peak gain = 1.29, Iterations = 63

Retrieve results for PID and form aggregate controller

CpidFinal = pid( getNominal(Cpid, CL) ), % PID block
Cfinal = getNominal(Call, CL);           % aggregate controller (pid + roll-off)

Continuous-time PIDF controller in parallel form:
 
           1            s    
Kp + Ki * --- + Kd * --------
           s          Tf*s+1 
 
With Kp = 1.02, Ki = 0.796, Kd = 0.298, Tf = 0.000456

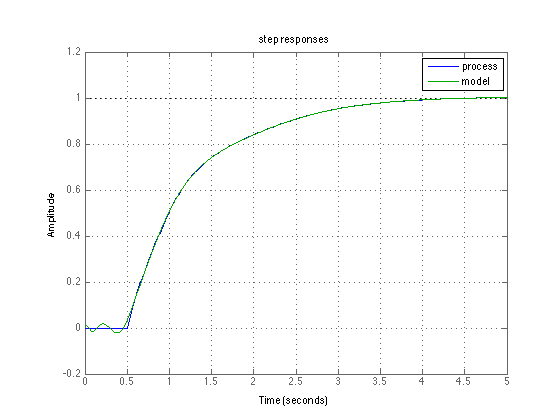
Show step responses of process and approximate model

Tprocess = feedback(Gprocess*Cfinal,1);
Tmodel   = feedback(Gmodel*Cfinal,1);
step(Tprocess,Tmodel,5); grid on; legend('process','model') ; title('step responses');

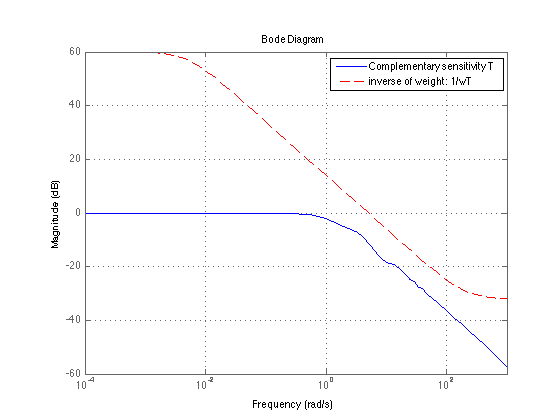
Check roll-off property

bodemag(Tprocess,1/wT,'r--'); grid on; legend('Complementary sensitivity T','inverse of weight: 1/wT') ;