hinfstruct vs. hinfsyn. Do the stats.

Compare hinfsyn and hinfstruct for controllers of the same order over nRand randomized problems.

Contents

Generate problems and run hinfstruct and hinfsyn

nRand = 10; % number of random problems
nx = 8; ny = 3; nu = 2; nw = 2; nz = 3; % plant dimensions
gamHINFSTRUCT = zeros(nRand,1); gamHINFSYN = zeros(nRand,1);

for ii=1:nRand
    P = rss(nx,nz+ny,nw+nu); % generate random plant
    C0 = ltiblock.ss('C0', nx, nu, ny); % state-space controller of order nx
    CL0 = lft(P,C0);
    % Run |hinfstruct|with 2 extra starting points
    op = hinfstructOptions('RandomStart', 2) ;       % add 2 starting points
    [CL1,gamHINFSTRUCT(ii)] = hinfstruct(CL0, op);   % CL1 is tuned version of CL0
    Cfinal = getNominal(C0, CL1);                    % retrieve final  controller
    gamHINFSTRUCT(ii) = norm( lft(P,Cfinal), inf);   % recompute to double check
    % Run |hinfsyn|
    [K,CL2,gamHINFSYN(ii)] = hinfsyn(P,ny,nu) ;
    gamHINFSYN(ii) = norm( lft(P,K), inf);           % recompute to double check
end

Final: Peak gain = 0.993, Iterations = 39
Final: Peak gain = 0.993, Iterations = 35
Final: Peak gain = 0.993, Iterations = 41
Final: Peak gain = 1.58, Iterations = 44
Final: Peak gain = 1.58, Iterations = 66
Final: Peak gain = 1.58, Iterations = 42
Final: Peak gain = 3.59, Iterations = 23
Final: Peak gain = 3.59, Iterations = 27
Final: Peak gain = 3.59, Iterations = 18
Final: Peak gain = 4.72, Iterations = 185
Final: Peak gain = 4.71, Iterations = 300
Final: Peak gain = 4.72, Iterations = 144
Final: Peak gain = 3.22, Iterations = 91
Final: Peak gain = 3.23, Iterations = 54
Final: Peak gain = 3.24, Iterations = 54
Final: Peak gain = 2.97, Iterations = 71
       Spectral radius 1.12e+05 is close to bound 1.45e+05
Final: Peak gain = 2.96, Iterations = 65
Final: Peak gain = 2.96, Iterations = 59
Final: Peak gain = 9.07, Iterations = 41
Final: Peak gain = 9.07, Iterations = 74
Final: Peak gain = 9.07, Iterations = 23
Final: Peak gain = 2.37, Iterations = 68
Final: Peak gain = 1.33, Iterations = 181
Final: Peak gain = 2.35, Iterations = 90
Final: Peak gain = 1.01, Iterations = 236
Final: Peak gain = 1.05, Iterations = 162
Final: Peak gain = 1.06, Iterations = 129
Final: Peak gain = 4.15, Iterations = 157
Final: Peak gain = 4.08, Iterations = 74
Final: Peak gain = 4.08, Iterations = 30

Display relative gaps

bar(  (gamHINFSTRUCT-gamHINFSYN)./gamHINFSYN  ) ; grid on;
title([' bar diagram of relative gaps wrt. hinfsyn over ' num2str(nRand) ' test problems']);
xlabel('problem index');

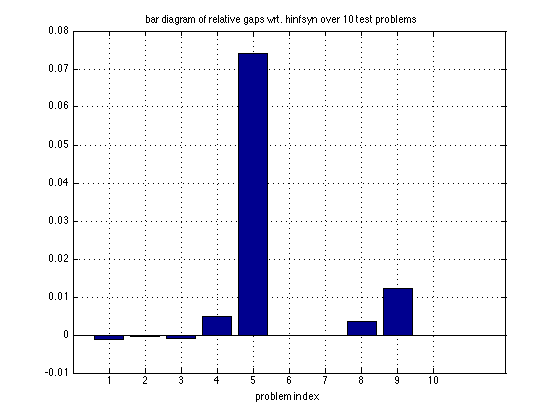
Compute mean relative gap over nRand test problems

Err1 = sum( (gamHINFSTRUCT-gamHINFSYN)./gamHINFSYN )/nRand ;
fprintf(1,'\n\n mean relative gap over %i test problems:  %6.2f \n\n', nRand,  Err1);


 mean relative gap over 10 test problems:    0.01

Remarks; global vs. local

Generally speaking, hinfsyn delivers globally optimal solutions to 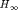$H_\infty$ synthesis problems proviso full-order controllers are acceptable. The achieved optimal value thus serves as a lower bound for those reached by hinfstruct. The nonsmooth programming technique hinfstruct implements a local technique. This means in particular that solutions are heavily dependent on the particular value of the initial point as well as critically on their number. A better local solution can therefore be obtained by employing multiple restarts. An optional argument is made available to that purpose:

op = hinfstructOptions('Randomstart', 2); % add 2 starting points to the default

Altogether we then have 3 = 2 + 1 starting points using the above syntax. Numerical testing indicates that 3 or 4 starting points is enough in most applications.


Published with MATLAB® 7.12